Нормальний розподіл – один з найважливіших розподілів імо- вірностей. Випадкові величини, що мають нормальний розпо- діл, розглядаються і використовуються у математичній стати- стиці, теорі¨ ймовірностей, імітаційному моделюванні, у числен- них задачах та застосуваннях науки і техніки.
Нормальний закон розподілу (розподіл Гауса) найчастіше зустрічається на практиці. Його використовують, коли випадкова величина залежить від великої кількості випадкових факторів, однорідних за своїм впливом, при цьому вплив кожного з них у порівнянні з усією їхньою сукупністю незначний.
Розподіл у якому всі три міри центральної тенденції збігаються – тобто середнє дорівнює медіані і дорівнює моді, називається нормальним (є ще інші характеристики нормального розподілу, але про них згодом – а ці є основними).
У розділі 1.5 ми розглянули різні гістограми і описали їх форми як симетричні, скошені вліво і перекошені вправо. Існує спеціальний симетричний розподіл форми, який називається нормальним розподілом. Він високо посередині, а потім швидко і однаково опускається на обох кінцях.
Нормальний розподіл Нормальний закон розподілу (normal law of distribution) (який ще називається законом Гаусса) відіграє виключно важливу роль в теорії ймовірностей і займає серед інших законів розподілу особливий стан.
Закон розподілу ймовірностей — це поняття теорії ймовірностей, яке для дискретної випадкової величини показує множину можливих подій з ймовірностями їхнього настання. Закон розподілу часто використовується для характеризування випадкової величини, яка має не дуже велику кількість реалізацій.

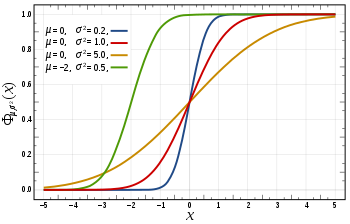
Нормальний розподіл (розподіл Ґауса) — розподіл ймовірностей випадкової величини, що характеризується густиною ймовірності $${\displaystyle f(x;\mu ,\sigma )={\frac {1}{\sigma {\sqrt {2\pi }}}}\,\exp \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)}$$де
Залишити відповідь